背景介绍
对于非RCT类的观察性研究,由于分组的非随机性,导致了研究偏倚的存在,致使观察到的效应很多时候往往并不可用。为了解决这个问题,研究者们提出了倾向性评分的方法,通过倾向性评分的计算,可以使得试验组和对照组之间的分布更加接近,从而减少了研究偏倚的影响。
我们公众号以往有过五篇类似的介绍内容,分别是:
其中,后面两篇文章提到了倾向性评分加权中的overlapping weighting方法,这篇文章将对倾向性评分加权的方法进行详细介绍。
因果效应
首先,我们来看下几种因果效应。
ATE即平均处理效应(average treatment effect),是指在试验组和对照组之间的处理效应的差异。理想情况下,随机对照试验估计出来的效应即ATE,但是在实际研究中,由于种种原因,我们往往无法进行随机对照试验。由于ATE的估计人群是试验组和对照组的总体,ATE假设两组受试者是有相同的概率/机会接受某一种处理的,然而,实际研究中,研究者往往更加关注的是ATE的局部估计,即在某一特定的人群中(一般是接受治疗的试验组),处理的效应是多少,而这个效应即为ATT(average treatment effect on the treated)。由于ATT只需要对处理组人群估计因果处理效应,对于RCT而言,潜在的治疗效果和治疗组分配是相互独立的,因此,ATT即为ATE;然而,对于非RCT类研究而言,二者是不同的。
我们还可以计算ATC(average treatment effect on the control),即对于未接受治疗的人群,如果接受治疗,其效应是多少。此外,还有ATM(average treatment effect among the evenly matchable),即在对照组中,找到与试验组相匹配的人群,计算在这个匹配的总体人群中的治疗效应;ATO(average treatment effect among the overlap population),即在试验组和对照组的重叠人群中,计算治疗效应。相比于ATM,ATO有着更好的方差属性,由于其不像ATM那样匹配要求,转而是选择两组重叠的中间人群,因此,ATO的估计更加稳健。
倾向性评分加权
针对以上五种因果效应,我们可以通过倾向性评分加权的方法来进行相应的估计。这里直接给出五种权重的计算公式:
- ATE:\(w_{ATE} = \frac{Z_i}{e_i} + \frac{1 - Z_i}{1 - e_i}\)
- ATT:\(w_{ATT} = \frac{e_iZ_i}{e_i} + \frac{e_i(1-Z_i)}{1-e_i}\)
- ATC:\(w_{ATC} = \frac{(1-e_i)Z_i}{e_i} + \frac{(1-e_i) (1-Z_i)}{1 - e_i}\)
- ATM:\(w_{ATC} = \frac{(1-e_i)Z_i}{e_i} + \frac{(1-e_i) (1-Z_i)}{1 - e_i}\)
- ATO:\(w_{AT0} = (1-e_i)Z_i + e_i(1-Z_i)\)
以上五种加权的示例以及具体实现的全部代码,我们已经放在了星球里,感兴趣的同学可以自行查看。
这里我们展示下加权后人群的分布情况。
原始人群的ps分布
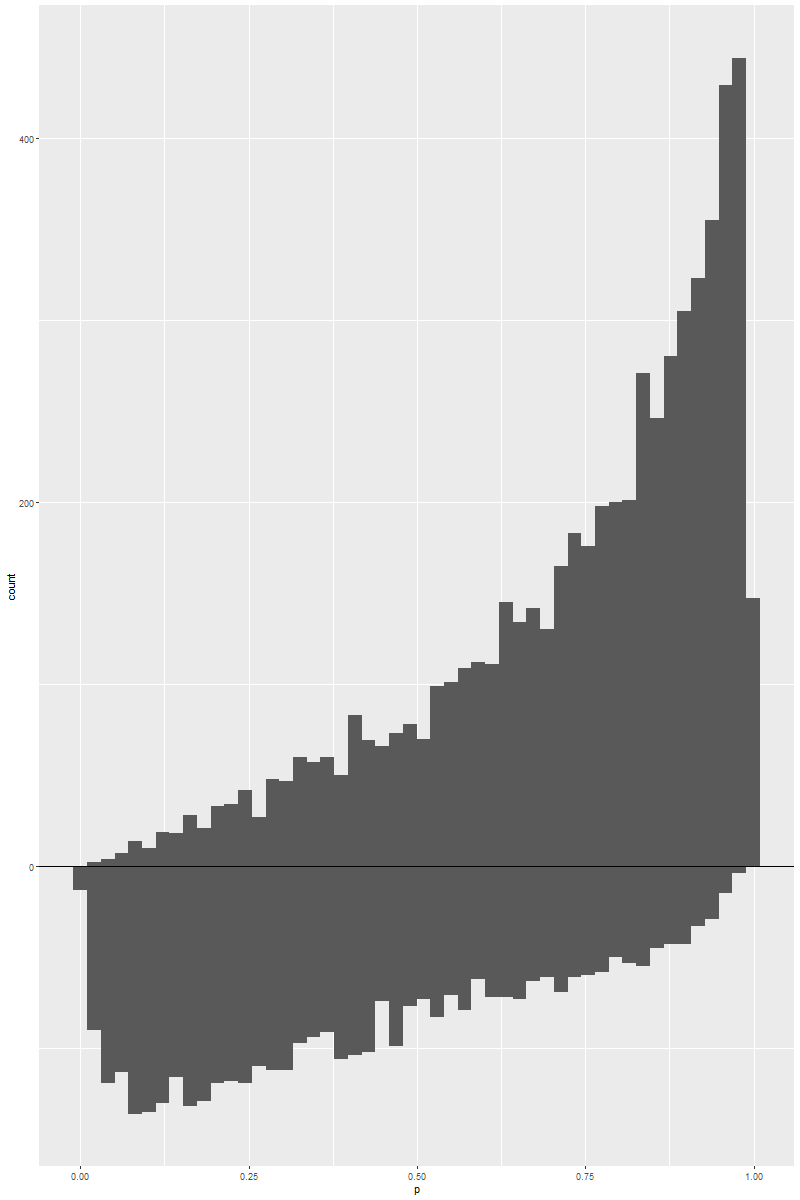
ATE
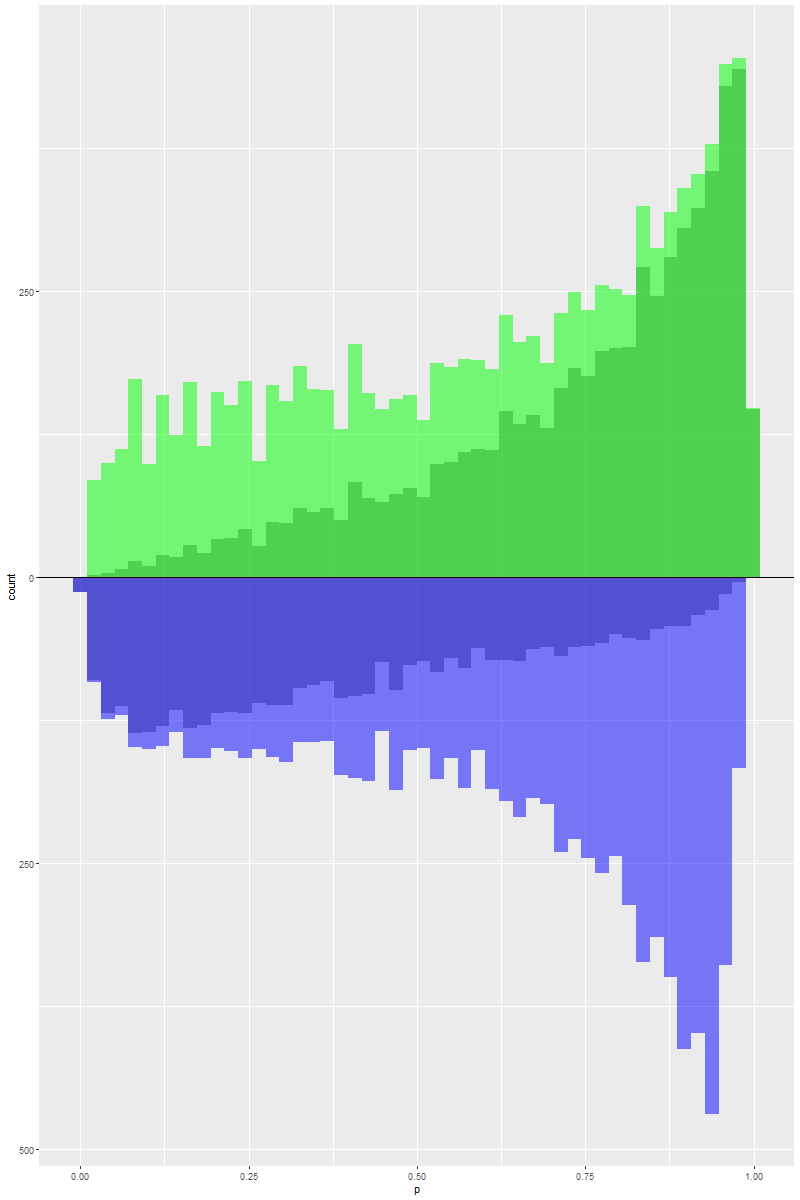
ATT
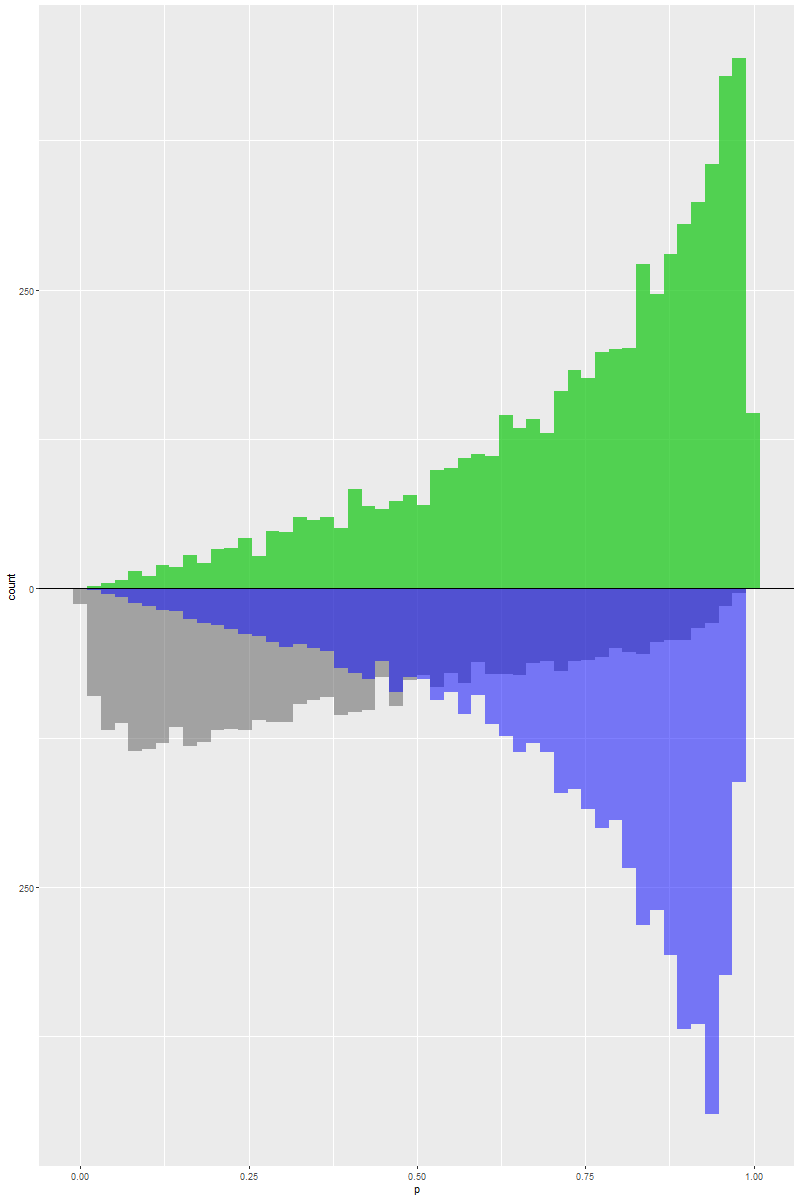
ATC
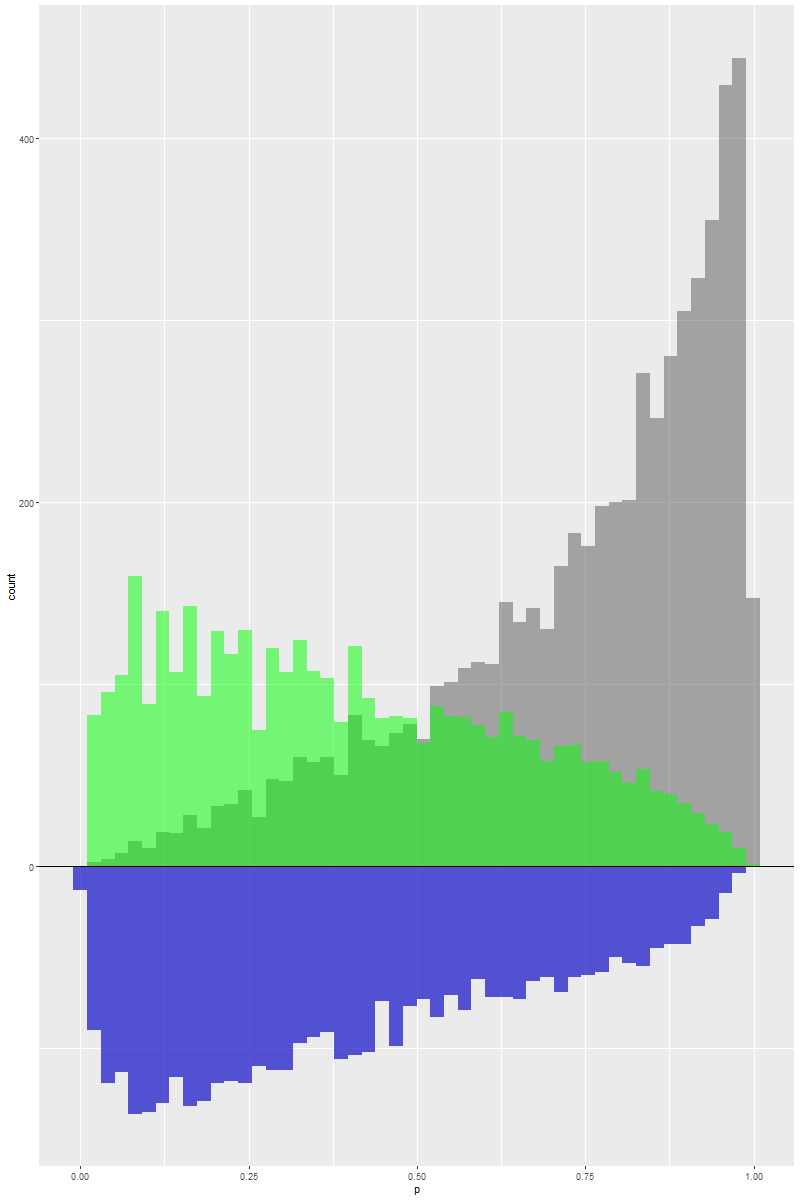
ATM
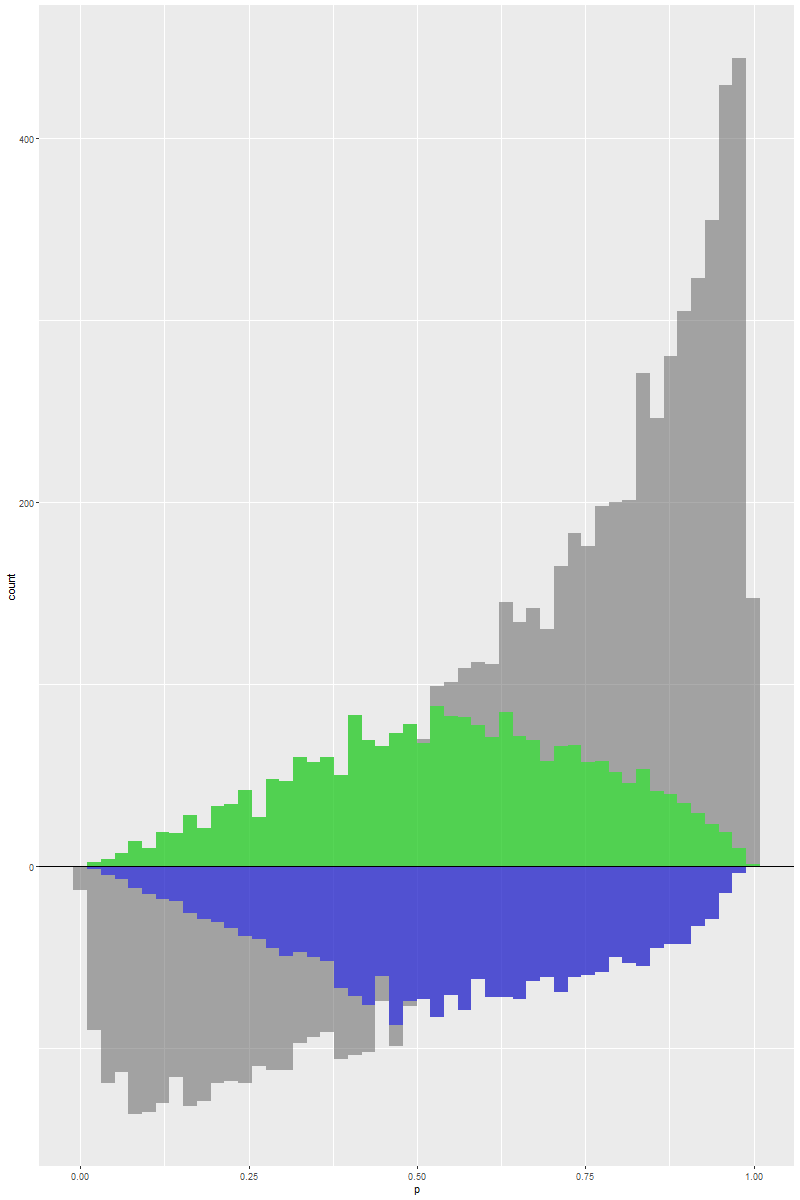
ATO
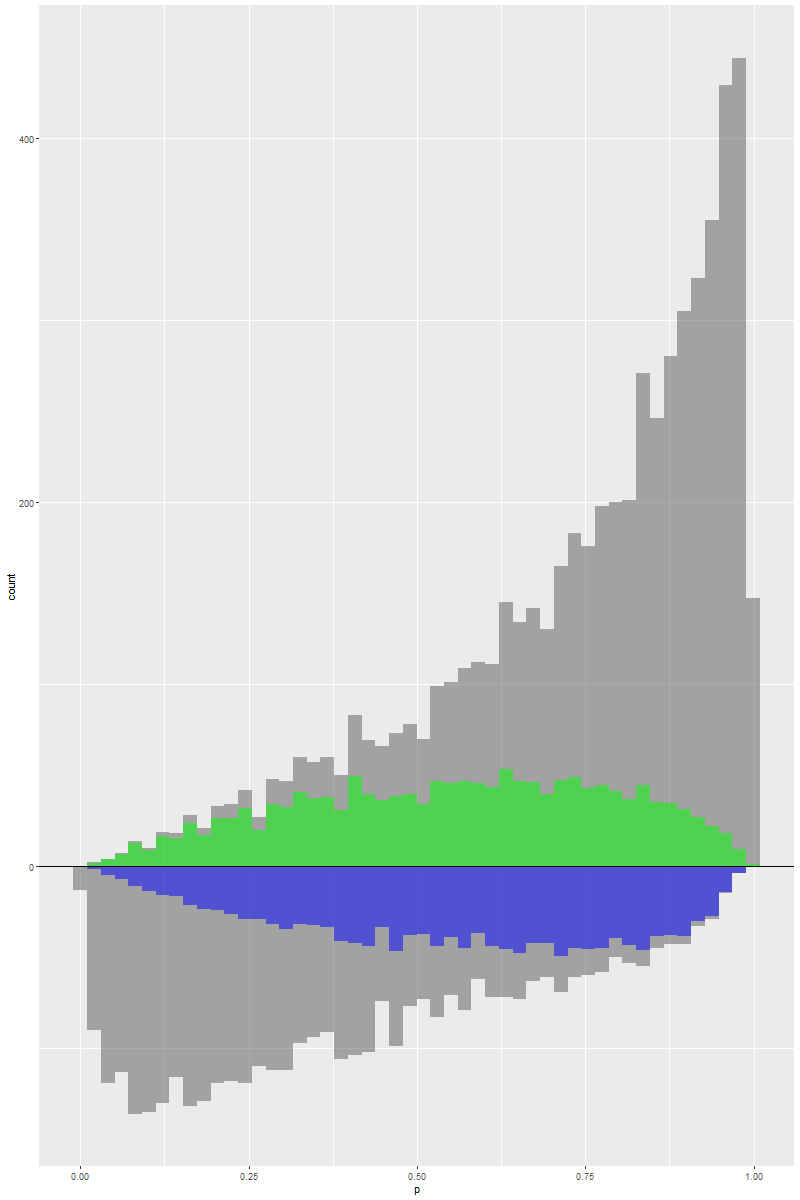
总结
相信通过以上可视化的展示,大家会更容易理解倾向性评分加权的方法对目标人群的选择以及治疗效应的解释。借助于合适的效应加权,我们可以估计出治疗效应并对于以上五种治疗效应的估计值。