NumPy 广播机制详解 | Zhen Lu

引言

这里我们介绍 NumPy 中的广播机制，这一功能是 NumPy 库的核心特性之一，特别适用于数据科学和数值计算领域，其允许不同形状的数组进行算术操作，显著简化代码并提升计算效率。

背景与定义

NumPy 是 Python 中用于高效数组操作的库，广泛应用于科学计算、机器学习和数据分析。广播机制是指 NumPy 在算术操作中处理不同形状数组的能力，通过扩展较小数组的维度，使其与较大数组匹配，从而进行逐元素操作。

例如，将标量 2 加到数组 [1, 2, 3] 上，结果为 [3, 4, 5]，标量 2 被概念上扩展为 [2, 2, 2]。这种机制不仅节省内存（不实际复制数据），还避免了手动循环，显著提高了计算效率，尤其在处理大型数据集时。

广播规则详解

广播的实现依赖于以下规则，确保数组形状兼容：

维度对齐：比较两个数组的形状，从右向左（尾部维度开始）。如果维度数不同，较小数组会在左侧补齐维度 1。例如，形状 (3,) 的数组可视为 (1, 3)。
形状兼容性：如果对应维度大小相等，直接操作。如果一个维度为 1，NumPy 会拉伸该维度，使其匹配另一个维度的大小。例如，形状 (1, 3) 的数组与 (2, 3) 相加，前者会被重复为 (2, 3)。如果对应维度既不等也不为 1，操作失败，抛出 ValueError，提示 operands could not be broadcast together。

结果形状：广播后的结果形状取每个维度的最大值，缺失维度视为 1。

例如：数组 A 形状 (2, 3)，数组 B 形状 (3,)：B 被视为 (1, 3)，然后广播为 (2, 3)，操作可进行。数组 C 形状 (2, 3)，数组 D 形状 (2, 2)：比较最后维度 3 和 2，不兼容，抛出错误。这些规则确保操作的正确性，但需要大家理解形状匹配的逻辑。

以下是几个具体例子，展示广播机制的应用：

import numpy as np
arr = np.array([1, 2, 3])
scalar = 2
result = arr + scalar
print(result)

[3 4 5]

这里，标量 2 被广播为 [2, 2, 2]，与 [1, 2, 3] 逐元素相加。效率高，因为不实际创建新数组。

arr1 = np.array([[1, 2, 3],
                 [4, 5, 6]])
arr2 = np.array([10, 20, 30])
result = arr1 + arr2
print(result)

[[11 22 33]
 [14 25 36]]

arr1 形状 (2, 3)，arr2 形状 (3,)。arr2 被视为 (1, 3)，然后广播为 (2, 3)，即 [[10, 20, 30], [10, 20, 30]]。结果为逐元素相加，符合预期。

在图像处理中，假设有形状 (2, 2, 3) 的图像数组（高度、宽度、通道），与形状 (3,) 的缩放向量：

image = np.array([[[0.8, 2.9, 3.9],
                   [52.4, 23.6, 36.5]],
                  [[55.2, 31.7, 23.9],
                   [14.4, 11.0, 4.9]]])
scale = np.array([3, 3, 8])
scaled_image = image * scale

scale 被广播为 (2, 2, 3)，每个像素的通道值分别乘以 [3, 3, 8]。这种操作在数据标准化或特征缩放中非常常见。

常见陷阱与优化建议

尽管广播强大，但有以下常见问题需要注意：

形状不匹配：如果数组形状无法广播，NumPy 会抛出 ValueError。建议先打印形状（如 print(arr.shape)）确认。
意外广播：一维数组与二维数组相加，可能按行或按列广播，需明确意图。例如，np.array([1,2]) + np.array([[3,4],[5,6]]) 需要注意广播方向。

a= np.array([1,2])
b= np.array([[3,4],[5,6]])
a + b
a[:, np.newaxis] + b

array([[4, 5],
       [7, 8]])

性能问题：对于大型数组，广播可能创建临时数组，增加内存使用。在内存受限情况下，考虑使用循环或显式重塑。

优化建议：

使用 np.newaxis 或 reshape 显式控制维度，例如 arr[:, np.newaxis] 将一维数组转为列向量。
检查数组形状，确保符合预期。
对于超大型数据集，评估广播是否会导致内存瓶颈，可能需要替代方案。

--- title: "NumPy 广播机制详解" date: 2025-03-25 description: "broadcasting in numpy" image: "https://cdn.jsdelivr.net/gh/Leslie-Lu/WeChatOfficialAccount/img_2025/broadcasting_2.png" categories: - python - numpy - broadcasting format: html: shift-heading-level-by: 1 include-in-header: - text: | <style type="text/css"> hr.dinkus { width: 50px; margin: 2em auto 2em; border-top: 5px dotted #454545; } div.column-margin+hr.dinkus { margin: 1em auto 2em; } </style> --- ## 引言这里我们介绍 NumPy 中的广播机制，这一功能是 NumPy 库的核心特性之一，特别适用于数据科学和数值计算领域，其允许不同形状的数组进行算术操作，显著简化代码并提升计算效率。 ## 背景与定义 NumPy 是 Python 中用于高效数组操作的库，广泛应用于科学计算、机器学习和数据分析。广播机制是指 NumPy 在算术操作中处理不同形状数组的能力，通过**扩展**较小数组的维度，使其与较大数组匹配，从而进行逐元素操作。例如，将标量 2 加到数组 [1, 2, 3] 上，结果为 [3, 4, 5]，标量 2 被概念上扩展为 [2, 2, 2]。这种机制不仅节省内存（不实际复制数据），还避免了手动循环，显著提高了计算效率，尤其在处理大型数据集时。 ## 广播规则详解广播的实现依赖于以下规则，确保数组形状兼容： - 维度对齐：比较两个数组的形状，从右向左（尾部维度开始）。如果维度数不同，较小数组会在左侧补齐维度 1。例如，形状 (3,) 的数组可视为 (1, 3)。 - 形状兼容性：如果对应维度大小相等，直接操作。如果一个维度为 1，NumPy 会**拉伸**该维度，使其匹配另一个维度的大小。例如，形状 (1, 3) 的数组与 (2, 3) 相加，前者会被重复为 (2, 3)。如果对应维度既不等也不为 1，操作失败，抛出 ValueError，提示 `operands could not be broadcast together`。 ![broadcasting](https://cdn.jsdelivr.net/gh/Leslie-Lu/WeChatOfficialAccount/img_2025/broadcasting_2.png) - 结果形状：广播后的结果形状取每个维度的最大值，缺失维度视为 1。例如：数组 A 形状 (2, 3)，数组 B 形状 (3,)：B 被视为 (1, 3)，然后广播为 (2, 3)，操作可进行。数组 C 形状 (2, 3)，数组 D 形状 (2, 2)：比较最后维度 3 和 2，不兼容，抛出错误。这些规则确保操作的正确性，但需要大家理解形状匹配的逻辑。以下是几个具体例子，展示广播机制的应用： ```{python} import numpy as np arr = np.array([1, 2, 3]) scalar = 2 result = arr + scalar print(result) ``` 这里，标量 2 被广播为 [2, 2, 2]，与 [1, 2, 3] 逐元素相加。效率高，因为不实际创建新数组。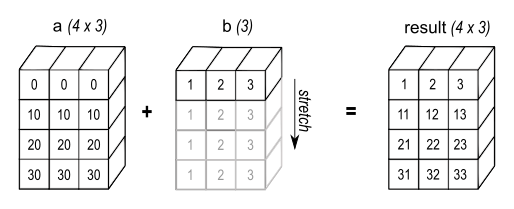 ```{python} arr1 = np.array([[1, 2, 3], [4, 5, 6]]) arr2 = np.array([10, 20, 30]) result = arr1 + arr2 print(result) ``` arr1 形状 (2, 3)，arr2 形状 (3,)。arr2 被视为 (1, 3)，然后广播为 (2, 3)，即 [[10, 20, 30], [10, 20, 30]]。结果为逐元素相加，符合预期。在图像处理中，假设有形状 (2, 2, 3) 的图像数组（高度、宽度、通道），与形状 (3,) 的缩放向量： ```{python} image = np.array([[[0.8, 2.9, 3.9], [52.4, 23.6, 36.5]], [[55.2, 31.7, 23.9], [14.4, 11.0, 4.9]]]) scale = np.array([3, 3, 8]) scaled_image = image * scale ``` scale 被广播为 (2, 2, 3)，每个像素的通道值分别乘以 [3, 3, 8]。这种操作在数据标准化或特征缩放中非常常见。 ## 常见陷阱与优化建议尽管广播强大，但有以下常见问题需要注意： - 形状不匹配：如果数组形状无法广播，NumPy 会抛出 ValueError。建议先打印形状（如 print(arr.shape)）确认。 - 意外广播：一维数组与二维数组相加，可能按行或按列广播，需明确意图。例如，np.array([1,2]) + np.array([[3,4],[5,6]]) 需要注意广播方向。 ```{python} a= np.array([1,2]) b= np.array([[3,4],[5,6]]) a + b a[:, np.newaxis] + b ``` - 性能问题：对于大型数组，广播可能创建临时数组，增加内存使用。在内存受限情况下，考虑使用循环或显式重塑。 ### 优化建议： - 使用 np.newaxis 或 reshape 显式控制维度，例如 arr[:, np.newaxis] 将一维数组转为列向量。 - 检查数组形状，确保符合预期。 - 对于超大型数据集，评估广播是否会导致内存瓶颈，可能需要替代方案。